Mobius: A Path to Ray Tracing

As one of my final classes at Waterloo I took Graphics (CS 488) with Gladimir Baranoski. When I first visited UW in 2013 a student referenced the course to me as one of the best undergraduate classes in the Computer Science department. It has been a challenging and rewarding experience and the most time-intensive project I have completed at university.
This is a description of the features I implemented along the way along with demonstrations and comparisons. I was inspired by some images I had seen of carved mobius tubes to try and create a ray tracer capable of simulating how light would pass through a glass mobius tube. With that in mind as the end goal, I set about implementing the following features.
Reflection
The first illumination model I implemented was phong illumination which shows diffuse colours and specular highlights of the material.
I extended the basic material model to include reflections like you would see in a mirror. We calculate the reflected ray which can be computed from the incoming ray and the normal of the surface it is intersecting. In order to make computation reasonable there is a limit on the number of reflections calculated. We track the depth of the reflection tree and cut it off after a specified number.




Glossy Reflection
Most reflective surfaces in real life are not perfect mirrors. Instead there are small perturbations in the surface that cause the reflections to be glossy. We can simulate this by slightly perturbing the reflected ray each time and averaging over a number of samples.


Soft Shadows
The initial illumination model only made use of point lights. In real life most lights cover a certain area which leads to softer shadows (unlike the hard shadows seen in the first few images). In order to implement soft shadows I created a new square area light which can be of any size. When checking to see if a surface is covered in shadow (by examining the path from the point to the light for obstacles) we can sample random points on the area light to determine how much of the surface is covered in shadow. Since this technique is ray-dependent, increasing the number of samples significantly improves the quality of the soft shadows.


Texture Mapping
In order to add detail that might be too costly to model, we can use texture mapping to paint images onto the primitives and meshes we’ve created. I implemented planar and spherical projection mapping which maps the points on the image to the 3D object of choice.


Refraction
Refraction gives us the option to simulate glass and other transparent materials. An index of refraction governs how much light bends after hitting the transparent material. The refraction implementation also includes a limit on how many times a given ray will refract before stopping in order to limit compute time.

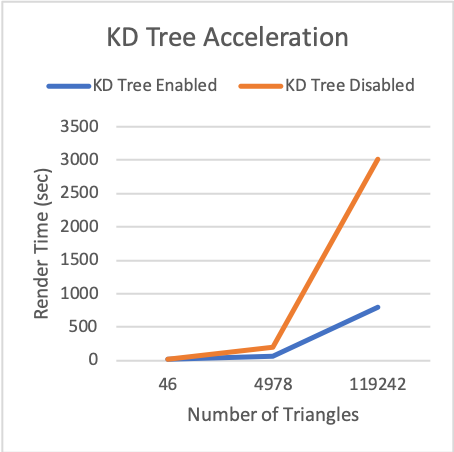
Acceleration with KD-Trees
The number of polygons in a scene is closely tied with how long the scene takes to render. In a naive implementation of a ray tracer every ray is tested against every primitive or polygon to see if they intersect. In order to reduce the number of intersection computations and speed up the renders I implemented a spatial subdivision with KD-Trees.
Spatial subdivision helps reduce the volume of the scene that is checked for intersections by each ray. A scene is split in ever smaller boundaries that encapsulate only a few objects. Since the ray only passes through a few of these boundaries, only a few objects need to be tested for intersections.
The KD-Tree chooses and axis and a splitting point at each node in the tree in order to refine the search area. A perfectly balanced KD-Tree (where every object is separable and every branch has the same number of objects) should take at most log n time to check for an intersection. I implemented a KD-Tree to store triangles for each mesh. Each triangle also stored a cube boundary which was used to calculate the cost of the splitting point. Each triangle boundary (in a given axis) is considered for the split and has a cost calculated, where the minimum cost is one which gives an equal number of objects on either side of the split.
The implemented KD-Tree shows significant speedups over the naive approach with high polygon counts.

Adaptive Antialiasing
Antialiasing removes jagged edges due to the low sampling rates (of rays) compared with high frequency objects (i.e. lots of detail in a single pixel). Adaptive antialiasing only chooses to increase the number of samples in areas of high contrast where aliasing is expected. To accomplish this a first pass is made with primary rays and the results are passed through a 2D laplacian filter checking for contrast. Pixels with high contrast passing a certain threshold are re-rendered with higher sample rates.



Path Tracing
Path tracing involves sampling light from all parts of the scene in order to create global illumination. Speedups can be made by randomly selecting paths to follow rather than calculating every possible path. I implemented a small approximation of this by randomly choosing a reflection or refrecration ray for the refracted materials. This creates the appearance of the fresnel effect on refracted materials and performs path tracing. It would be great to extend this to do proper global illumination from diffuse surfaces as well.


Additional features
- Multithreading: batching rays in threads enables much faster rendering. By observation I saw 10-100x speedups on some scenes by using hyperthreading to run up to 512 simultaneous threads.
- Animations: the lua scripting languages is used to provide scene descriptions. I created animations by calling the render function multiple times in sequence for each scene and manipulating transformations according to the given timestep. See the video below for examples.
Worth Reading
Here are papers and websites I referenced during my research and implementation of this ray tracer. There are a lot of really good books on the subject, but I especially enjoyed the PBR book.
-
James F. Blinn and Martin E. Newell. Texture and reflection in computer generated images. Communications of the ACM, 19(10):542 547, October 1976.
-
R. Cook, T. Porter, and L. Carpenter. Distributed ray tracing. Computer Graphics, 18(3):137–145, July 1984
-
M. Pharr, W. Jakob, and G. Humphreys. Physically Based Rendering: From Theory to Implementation. 3ed, October 15, 2018. Retrieved from [http://www.pbr-book.org/]
-
J. Painter and K. Sloan. Antialiased ray tracing by adaptive progressive refinement. Computer Graphics, 23(3):281–288, July 1989.
-
Mitchell, Don P. Generating Antialiased Images at Low Sampling Densities. Computer Graphics 21(4):65-69, July, 1987.
-
K. Suffern. Ray Tracing from the Ground Up. A K Peters/CRC Press. Pages 529-542. 2007. Retrieved from [http://www.raytracegroundup.com/downloads/Chapter25.pdf]
-
J.T. Kajiya. The rendering equation. Computer Graphics, 20(3):143–150, August 1986.
-
H. W. Jensen and P. Christensen. Efficient simulation of light transport in scenes with participating media using photon maps. Computer Graphics (SIGGRAPH) Proceedings, pages 311–320, July 1998.
-
Z. Waters. Photon Mapping. Retrieved from [https://web.cs.wpi.edu/~emmanuel/courses/cs563/write_ups/zackw/photon_mapping/PhotonMapping.html].
-
S.M. Rubin and T.A. Whitted. Three-dimensional representation for fast rendering of complexscenes. Computer Graphics, 14(3):110–116, July 1980
-
B. Smits. Efficiency Issues for Ray Tracing. Journal of Graphics Tools, 3(2):1–14, 1998.
Putting it all together
To conclude, here is a short film of the progression of the Mobius ray tracer.
Mobius (The Path to Ray Tracing) from Jonathan Smith.
The final scene which I set out to create was a glass mobius strip. I modeled lily pads to garnish the surface and lit the model against a plane with a water texture mapped to it.
