Real Neural Networks
Over one hundred years ago a neuroscientist named Louis Lapicque published Recherches quantitatives sur l’excitation électrique des nerfs tratée comme une polarisation in which he described a mathematical model of a neuron which has become one of the most popular and longstanding representations of the way our brains store and communicate information. Since then scientists have uncovered many of the specific chemical and electrical mechanisms that occur in our minds. This research has been co-opted for many different fields ranging from social science to computer science. Here we will take a brief look at the mathematical functions used in the original integrate-and-fire model of the neuron and other related models before comparing them to the current work in artificial neural networks.
In computer science, artificial neural networks have proven to be useful for approximating many mathematical functions allowing computers to learn representations and infer solutions to a multitude of problems based on available data. These are powerful tools because they allow the circumvention of computing exact solutions or even formulating strict problem definitions. In light of this, there has been a rapid application of neural networks, leaving lots of the theory behind their success to still be developed. As we investigate their theory, we can continue to be inspired the biological systems that originally formed the impetous for the creation of artificial neural networks.
The Hundred Year Model
More than one hundred years ago (1907) a neuron model was developed that is still used today. This was the integrate-and-fire model created by Lapicque and summarized well in English by L.F. Abbott. The strength of Lapicque’s idea was in creating an analogy between a neuron and an electric circuit. This is outlined in the diagram from Abbot’s review of the model:
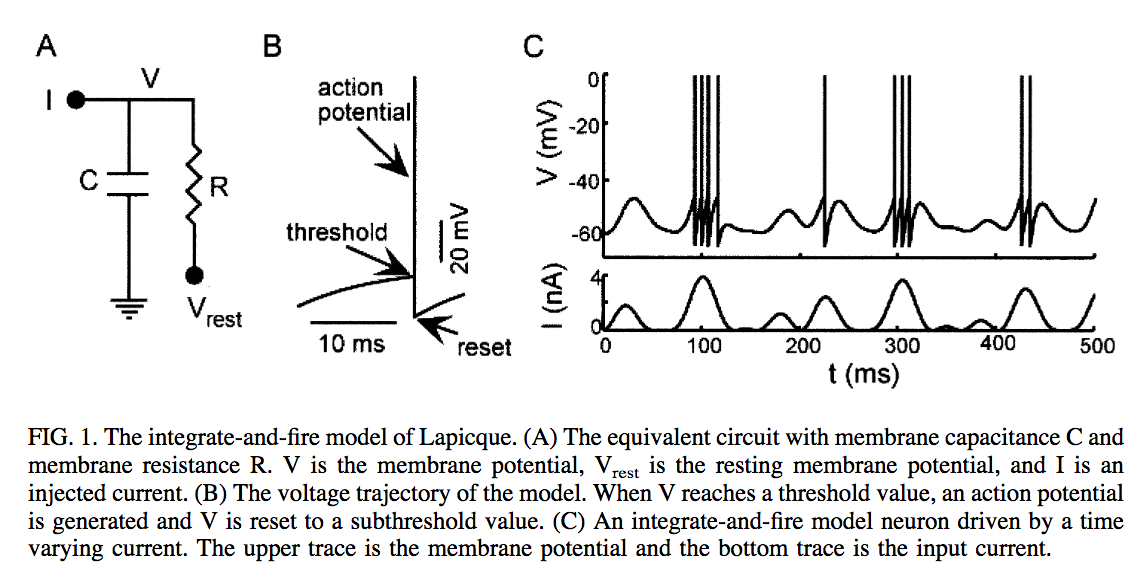
This model is often used when explaining the properties of large real neural networks where the minutiea of the individual interactions are less important than the overall system. A neuron with a reseting period (which limits how often a neuron can spike) can have its firing frequency modeled as a function of a constant input current:
\[f(I) = \frac{I}{C_m V_{th} + t_{ref} I}\]This model lacks the idea of time-dependant memory, which we shall see is very helpful in fully modeling real neural networks.
Hodgkin & Huxley
In 1952 two scientists with the initials A.H. published some papers outlining how nerve cells communicate with each other using action potentials or spikes. The final paper described “the flow of electric current through the surface membrane of a giant nerve fibre” as mathematical functions. By 1963 people realized this was very useful discovery and they gave Alan Hodgkin and Andrew Huxley (and a third scientist, Sir John Eccles) a Nobel Prize.
In the Hodgkin-Huxley model of the neuron, sodium and potassium ions pass through chemical channels in the cell membrane and their movements (as well as other leakages) cause changes in charge. Ion currents are defined by their conductances (\(g\)) and are dependant on the number of channel gates open or closed (the probability of a single gate being open is \(m, n, h\)). The change in membrane potential (\(V\)) can then be represented by the following equation:
\[c \frac{dV}{dt} = J_{in} - g_L (V - V_L) - g_{Na} m^3 h (V - V_{Na}) - g_K n^4 (V - V_K)\]Which could probably use some descriptions:
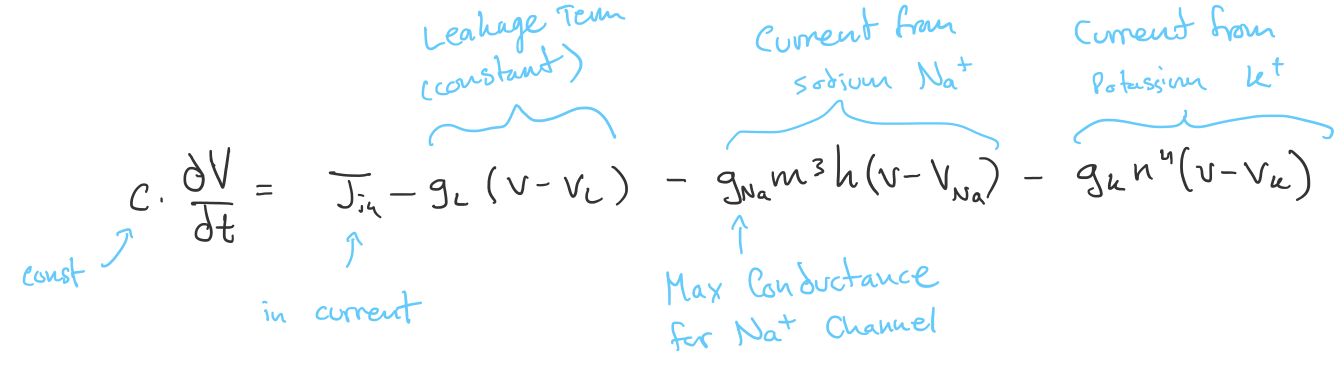
This translates into a system of four differential equations (when including the three equations for the fraction of gates open) which can describe the action potential of neurons. As the action potential increases, the voltage of a neuron spikes and neurotransmitters are released from one end of a neuron (the dendrites) and attach to the synapses of another, which is what actually passes information between neurons. This process is even more complicated that what the Hodgkin-Huxley model encompasses, but the model is useful because it shows the link between the original integrate-and-fire model and the more accurate used Leaky integrate-and-fire model.
Leaky integrate-and-fire
The leaky integrate-and-fire model of a neuron considers only the sub-threshold membrane potential without modeling the spike itself. This allows us to record when a spike occurs and provide a reset time before we start integrating over the input current again. The differential equation can be derived using part of the Hodgkin-Huxley equation (\(V_L\) is the voltage threshold for a spike):
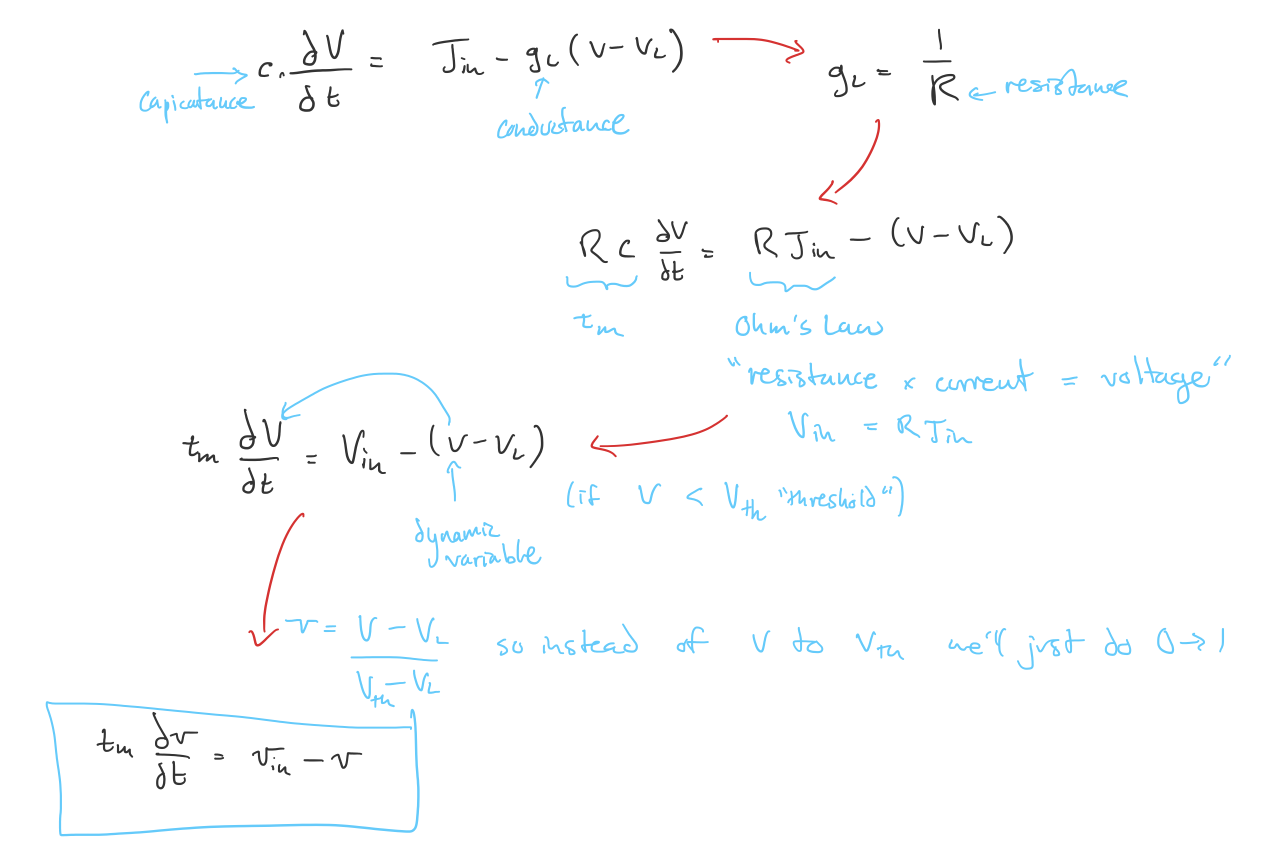
What’s Next
I’d like to extend this by showing how we can use filtered spike trains based on the Leaky integrate-and-fire model to calculate post-synaptic current across many neurons and model entire networks. Then I would like to compare that with the classica artificial neural network models.
References
There were many resources I tapped on to put together this article. They include the following:
- L. Lapicque. (1907) Recherches quantitatives sur l’excitation électrique des nerfs tratée comme une polarisation
- L. F. Abbot. (1999) Lapicque’s Introduction of the integrate-and-fire model neuron (1907)
- J. Orchard. (2019) CS489: Special Topics in Neural Networks Lectures
- A. L. Hodgkin and A. F. Huxley. (1952) A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve
- Markus Gesmann. (2012) Hodgkin-Huxley model in R